Summary and Analysis of Extension Program Evaluation in R

Salvatore S. Mangiafico

Converting Numeric Data to Categories

There are occasions when it is useful to categorize Likert scores, Likert scales, or continuous data into groups or categories.  In general, there are no universal rules for converting numeric data to categories.  A few methods are presented here.

Categorizing data by a range of values

One approach is to create categories according to logical cut-off values in the scores or measured values.  An example of this is the common grading system in the U.S. in which a 90% grade or better is an “A”, 80–89% is “B”, etc.  It is common in this approach to make the categories with equal spread in values.  For example, there is a 10 point spread in a “B” grade and a 10 point spread in a “C” grade.  But this equality is not required.  Below in the “Categorize data by range of values” example, 5-point Likert data are converted into categories with 4 and 5 being “High”, 3 being “Medium”, and 1 and 2 being “Low”.

This approach relies on the chosen cut-off points being meaningful.  For example, for a grade of 70–79 to be considered “sufficient”, the evaluation instruments (e.g. the tests, quizzes, and assignments) need to be calibrated so that a grade of 75 really is “sufficient”, and not “excellent” or “good”, etc.   You can imagine a case where a 4 or 5 on a 5-point Likert item is considered “high”, but if all respondents scored 4 or 5 on the item, it might not be clear that these values are “high”, but may just be the typical response.  Likewise, in this case, the decision to group 4 and 5 as “high” needs be compared with a decision to group 4 with 2 and 3 as “medium”.  This breakdown may be closer to how people interpret a 5-point Likert scale.  Either grouping could be meaningful depending on the purpose of the categorization and the interpretation of each level in the Likert item.

Categorizing data by percentiles

A second approach is to use percentiles to categorize data.  Remember, the value for the 90^th percentile is the score or measurement below which 90% of respondents scored. 

The advantage to this approach is that it does not rely on the scoring system being meaningful in its absolute values.  That is, students scoring above the 90^th percentile are scoring higher than 90% of students.  It doesn’t matter if the score for the 90^th percentile is 90 out of 100 or 50 out of 100.  If the groups use equally-spaced breakpoints, for example 0^th, 25^th, 50^th, 75^th, and 100^th percentiles, there should be approximately an equal number of respondents in each category.

Categorizing data with clustering

A third approach is to use a clustering algorithm to divide data into groups with similar measurements.  This is useful when there are multiple measurements for an individual.  For example, if students receive scores on reading, math, and analytical thinking, an algorithm can determine if, for example, there is a group of students who do well on all three measurements, and a group of students who do well in math and analysis but who do poorly on reading.  Most clustering algorithms assume that measurement data is continuous in nature.  Below, the partitioning around medoids (PAM) method is used with the manhattan metric.  This may be relatively more suitable for ordinal data than some other methods

Packages used in this chapter

The packages used in this chapter include:

•  psych

•  cluster

•  fpc

The following commands will install these packages if they are not already installed:

if(!require(psych)){install.packages("psych")}
if(!require(cluster)){install.packages("cluster")}
if(!require(fpc)){install.packages("fpc")}

Examples for converting numeric data to categories

Input =("
Instructor  Student  Likert
 Homer      a        3
 Homer      b        4
 Homer      c        4
 Homer      d        4
 Homer      e        4
 Homer      f        5
 Homer      g        5
 Homer      h        5
 Homer      i        3
 Homer      j        2
 Homer      k        3
 Homer      l        4
 Homer      m        5
 Homer      n        5
 Homer      o        5
 Homer      p        4
 Homer      q        4
 Homer      r        3
 Homer      s        2
 Homer      t        5
 Homer      u        3
")

Data = read.table(textConnection(Input),header=TRUE)


###  Check the data frame

library(psych)

headTail(Data)

str(Data)

summary(Data)


### Remove unnecessary objects

rm(Input)

Categorize data by range of values

The following example will categorize responses on a single 5-point Likert item.   The algorithm will be a score of 1 or 2 will be called “low”, a score of 3 “medium”, and a score of 4 or 5 “high”.

Categorize data

Data$Category[Data$Likert == 1 | Data$Likert == 2] = "Low"
Data$Category[Data$Likert == 3                   ] = "Medium"
Data$Category[Data$Likert == 4 | Data$Likert == 5] = "High"

Data

Order factor levels to make output easier to read

Data$Category = factor(Data$Category,
                    levels=c("Low", "Medium", "High"))

Summarize counts of categories

XT = xtabs(~ Category + Instructor,
           data = Data)

XT

        Instructor
Category Homer
  Low        2
  Medium     5
  High      14

Report students in each category

Data$Student[Data$Category == "Low"]

[1] j s

Data$Student[Data$Category == "Medium"]

[1] a i k r u

Data$Student[Data$Category == "High"]

[1] b c d e f g h l m n o p q t

Alternate method with tapply

tapply(X     = Data$Student,
       INDEX = Data$Category,
       FUN   = print)

$Low
[1] j s

$Medium
[1] a i k r u

$High
 [1] b c d e f g h l m n o p q t

Summary table

Category   Range     Count  Students
Low        1 or 2     2     j, s
Medium     3          5     a, i, k, r, u
High       4 or 5    14     b, c, d, e, f, g, h, l, m, n, o, p, q, t

Categorize data by percentile

The following example will categorize responses on a single 5-point Likert item.  Respondents scoring below the 33^rd percentile will be labeled “Lower third”; those between the 33^rd and 67^th percentile “Middle third”; and those above the 67^th percentile “Upper third”.

Categorize data

Percentile_00  = min(Data$Likert)
Percentile_33  = quantile(Data$Likert, 0.33333)
Percentile_67  = quantile(Data$Likert, 0.66667)
Percentile_100 = max(Data$Likert)


RB = rbind(Percentile_00, Percentile_33, Percentile_67, Percentile_100)

dimnames(RB)[[2]] = "Value"

RB

                Value
Percentile_00  2.0000
Percentile_33  3.6666
Percentile_67  4.3334
Percentile_100 5.0000

Data$Group[Data$Likert >= Percentile_00 & Data$Likert <  Percentile_33]  = "Lower_third"
Data$Group[Data$Likert >= Percentile_33 & Data$Likert <  Percentile_67]  = "Middle_third"
Data$Group[Data$Likert >= Percentile_67 & Data$Likert <= Percentile_100] = "Upper_third"

Data

Order factor levels to make output easier to read

Data$Group = factor(Data$Group,
                    levels=c("Lower_third", "Middle_third", "Upper_third"))

Summarize counts of groups

XT = xtabs(~ Group + Instructor,
           data = Data)

XT

              Instructor
Group          Homer
  Lower_third      7
  Middle_third     7
  Upper_third      7

Report students in each group

 tapply(X     = Data$Student,
        INDEX = Data$Group,
        FUN   = print)

$Lower_third
[1] a i j k r s u

$Middle_third
[1] b c d e l p q

$Upper_third
[1] f g h m n o t

Summary table

Group         Range       Count  Students
Lower third   1, 2, or 3  7      a, i, j, k, r, s, u
Middle third  4           7      b, c, d, e, l, p, q
Upper third   5           7      f, g, h, m, n, o, t

Categorize data by clustering

In the following example, each student has a score for Happy and for Tired.  The students will be divided into clusters based on the similarities of their scores across both measures.

Example data

Input =("
Instructor  Student  Happy   Tired
Marge       a        5       5
Marge       b        5       5
Marge       c        2       5
Marge       d        2       5
Marge       e        5       5
Marge       f        5       5
Marge       g        1       5
Marge       h        1       5
Marge       i        1       5
Marge       j        5       5
Marge       k        3       3
Marge       l        3       3
Marge       m        3       3
Marge       n        5       2
Marge       o        5       2
Marge       p        5       1
Marge       q        5       1
Marge       r        5       1
Marge       s        4       1
Marge       t        4       1
")

Data = read.table(textConnection(Input),header=TRUE)


###  Check the data frame

library(psych)

headTail(Data)

str(Data)

summary(Data)


### Remove unnecessary objects

rm(Input)

Plot data

In the following plot, each letter represents a Student from the data frame.  To me, this plot suggests that the data could be reasonably clustered into 4 or perhaps 7 or 8 clusters.

plot(jitter(Happy) ~ jitter(Tired),
     data = Data,
     pch=as.character(Data$Student))

Use only numeric data

Data.num = Data[c("Happy", "Tired")]

Determine the optimal number of clusters

The pamk function in the fpc package can determine the optimum number of clusters for the partitioning around medoids (PAM) method.  It will also complete the PAM analysis, but we’ll do that separately below. 

Practical considerations may override the results of the pamk function.  In the example below, if we include 1 in the possible range of cluster numbers, the function will determine that 1 is the optimum number.  Also, if we extend the range to, say, 10, the function will choose 7 as the optimum number, but this may be too many for our purposes.

library(fpc)

PAMK = pamk(Data.num,
            krange = 2:5,
            metric="manhattan")

PAMK$nc

[1] 4

   ###  This is the optimum number of clusters in the range

plot(PAMK$crit)
lines(PAMK$crit)

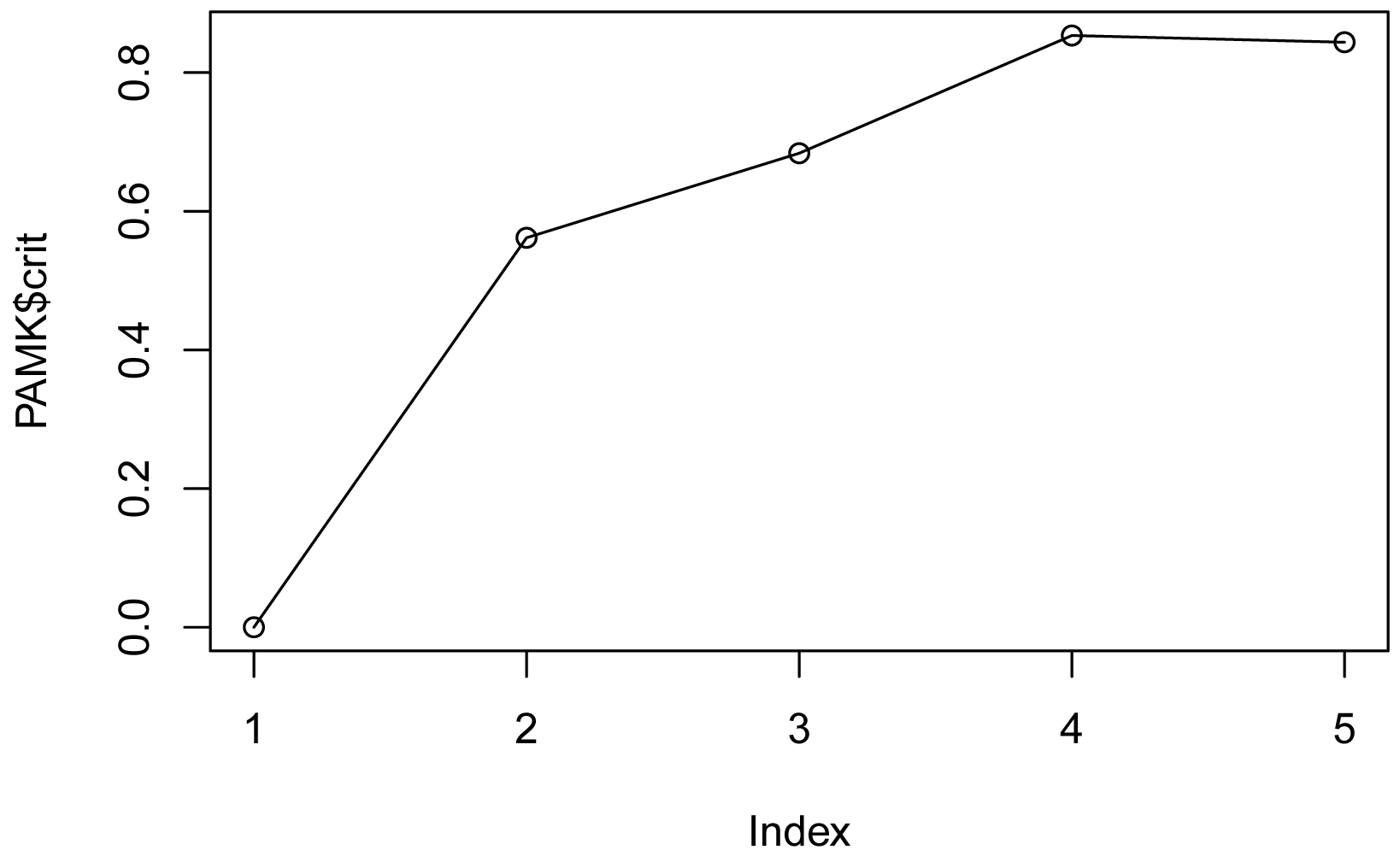
For the range of cluster numbers shown on the x-axis, the crit value is maximized at 4, suggesting 4 is optimum number of clusters for this range.

Categorize data

We will use the pam function in the cluster package to divide our data into four clusters.

library(cluster)

PAM = pam(x = Data.num,
          k = 4,              ### Number of clusters to find
          metric="manhattan")

PAM

Medoids:
     ID Happy Tired
[1,] 10     5     5
[2,]  9     1     5
[3,] 13     3     3
[4,] 16     5     1

Clustering vector:
 [1] 1 1 2 2 1 1 2 2 2 1 3 3 3 4 4 4 4 4 4 4

### Add clusters to data frame

PAMClust = rep("NA", length(Data$Likert))

PAMClust[PAM$clustering == 1] = "Cluster 1"
PAMClust[PAM$clustering == 2] = "Cluster 2"
PAMClust[PAM$clustering == 3] = "Cluster 3"
PAMClust[PAM$clustering == 4] = "Cluster 4"


Data$Cluster = PAMClust

Data

Order factor levels to make output easier to read

Data$Cluster = factor(Data$Cluster,
                      levels=c("Cluster 1", "Cluster 2",
                               "Cluster 3", "Cluster 4"))

Summarize counts of groups

XT = xtabs(~ Cluster + Instructor,
           data = Data)

XT

           Instructor
Cluster     Marge
  Cluster 1     5
  Cluster 2     5
  Cluster 3     3
  Cluster 4     7

Report students in each group

 tapply(X     = Data$Student,
        INDEX = Data$Cluster,
        FUN   = print)

$`Cluster 1`
[1] a b e f j

$`Cluster 2`
[1] c d g h i

$`Cluster 3`
[1] k l m

$`Cluster 4`
[1] n o p q r s t

Summary table

Cluster         Interpretation       Count  Students
Cluster 1     Tired and happy      5      a, b, e, f, j
Cluster 2     Tired and not happy  5      c, d, d, h, i
Cluster 3     Middle of the road   3      k, l, m
Cluster 4     Not tired and happy  7      n, o, p, q, r, s, t

Final plot

ggplot(Data,
       aes(x     = Tired,
           y     = Happy,
           color = Cluster)) +
   geom_point(size=3) +
   geom_jitter(width = 0.4, height = 0.4) +
   theme_bw()

©2016 by Salvatore S. Mangiafico.
Rutgers Cooperative Extension, New Brunswick, NJ.
Updated: 2025.

Non-commercial reproduction of this content, with attribution, is permitted.
For-profit reproduction without permission is prohibited.

If you use the code or information in this site in a published work, please cite it as a source.  Also, if you are an instructor and use this book in your course, please let me know.   My contact information is on the About the Author of this Book page.

Citation

Mangiafico, S.S. 2016. Summary and Analysis of Extension Program Evaluation in R, version 1.23.1, revised 2025. rcompanion.org/handbook/. (Pdf version: rcompanion.org/documents/RHandbookProgramEvaluation.pdf.)