An R Companion for the Handbook of Biological Statistics

Salvatore S. Mangiafico

Simple Logistic Regression

 

When to use it

Null hypothesis

How the test works

Assumptions

 

See the Handbook for information on these topics.

 

Examples

 

The Mpi example is shown below in the “How to do the test” section.

 

Graphing the results

Similar tests

 

See the Handbook for information on these topics.

 

Packages used in this chapter

 

The following commands will install these packages if they are not already installed:

if(!require(car)){install.packages("car")}
if(!require(lmtest){install.packages("lmtest")}
if(!require(tidyr)){install.packages("tidyr")}
if(!require(rcompanion)){install.packages("rcompanion")}
if(!require(FSA){install.packages("FSA")}
if(!require(popbio)){install.packages("popbio")}

 

 

How to do the test

 

Logistic regression can be performed in R with the glm (generalized linear model) function.  This function uses a link function to determine which kind of model to use, such as logistic, probit, or

Poisson.  These are indicated in the family and link options.  See ?glm and ?family for more information.

 

Assumptions

Generalized linear models have fewer assumptions than most common parametric tests.  Observations still need to be independent, and the correct link function needs to be specified.  So, for example you should understand when to use a poisson regression, and when to use a logistic regression.  However, the normal distribution of data or residuals is not required.

 

Specifying the counts of “successes” and “failures”

Logistic regression has a dependent variable with two levels.  In R, this can be specified in three ways.  1) The dependent variable can be a factor variable where the first level is interpreted as “failure” and the other levels are interpreted as “success”.  (As in the second example in this chapter).  2) The dependent variable can be a vector of proportions of successes, with the caveat that the number of observations for each proportion is indicated in the weights option.  3) The dependent variable can be a matrix with two columns, with the first column being the number of “successes” and the second being the number of “failures”.  (As in the first example in this chapter).

 

Not all proportions or counts are appropriate for logistic regression analysis

Note that in each of these specifications, both the number of successes and the number of failures is known.  You should not perform logistic regression on proportion data where you don’t know (or don’t tell R) how many individuals went into those proportions.  In statistics, 75% is different if it means 3 out of 4 rather than 150 out of 200.  As another example where logistic regression doesn’t apply, the weight people lose in a diet study expressed as a proportion of initial weight cannot be interpreted as a count of “successes” and “failures”.  Here, you might be able to use common parametric methods, provided the model assumptions are met; log or arc-sine transformations may be appropriate.  Likewise, if you count the number of people in front of you in line, you can’t interpret this as a percentage of people since you don’t know how many people are not in front of you in line.  In this case with count data as the dependent variable, you might use poisson regression. 

 

Overdispersion

One potential problem to be aware of when using generalized linear models is overdispersion.  This occurs when the residual deviance of the model is high relative to the residual degrees of freedom.  It is basically an indication that the model doesn’t fit the data well. 

 

It is my understanding, however, that overdispersion is technically not a problem for a simple logistic regression, that is one with a binomial dependent and a single continuous independent variable.  Overdispersion is discussed in the chapter on Multiple logistic regression.

 

Pseudo-R-squared

R does not produce r-squared values for generalized linear models, and common r-squared are not defined for these models. However, a variety of pseudo r-squared measures can be reported.

 

My function nagelkerke will calculate the McFadden, Cox and Snell, and Nagelkereke pseudo r-squared for glm and other model fits.  The Cox and Snell is also called the ML, and the Nagelkerke is also called the Cragg and Uhler.  These pseudo r-squared values compare the maximum likelihood of the model to a nested null model fit with the same method.  They should not be thought of as the same as the R-squared from an ordinary-least-squares linear (OLS) model, but instead as a relative measure among similar models.  The Cox and Snell and Efron’s pseudo R-squared for an OLS linear model, however, will be equivalent to R-squared for that model. 

 

Some authors recommend McFadden pseudo-R-squared for logistic regression.  (See the Cross Validated discussion in the References.)  Efron’s pseudo r-squared and count pseudo r-squared are also recommended (see IDRE in the References).

 

Testing for p-values

Note that testing p-values for a logistic or poisson regression uses Chi-square tests.  This is achieved through the test=“Wald” option in Anova to test the significance of each coefficient, and the test=“Chisq” option in anova for the significance of the overall model.  A likelihood ratio test can also be used to test the significance of the overall model.

 

Logistic regression example

 

### --------------------------------------------------------------
### Logistic regression, amphipod example, p. 247
### --------------------------------------------------------------

Input = ("
 Location           Latitude  mpi90  mpi100
 Port_Townsend,_WA  48.1        47    139
 Neskowin,_OR       45.2       177    241
 Siuslaw_R.,_OR     44.0      1087   1183
 Umpqua_R.,_OR      43.7       187    175
 Coos_Bay,_OR       43.5       397    671
 San_Francisco,_CA  37.8        40     14
 Carmel,_CA         36.6        39     17
 Santa_Barbara,_CA  34.3        30      0
")

Data = read.table(textConnection(Input),header=TRUE)

Data$Total = Data$mpi90 + Data$mpi100

Data$Percent = Data$mpi100 / + Data$Total

 

 

Model fitting

 

Trials = cbind(Data$mpi100, Data$mpi90)         # Sucesses, Failures

model = glm(Trials ~ Latitude,
            data = Data,
            family = binomial(link="logit"))

 

 

Coefficients and exponentiated cofficients

summary(model)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept) -7.64686    0.92487  -8.268   <2e-16 ***
Latitude     0.17864    0.02104   8.490   <2e-16 ***

 

confint(model)

                 2.5 %     97.5 %
(Intercept) -9.5003746 -5.8702453
Latitude     0.1382141  0.2208032

 

exp(model$coefficients)         # exponentiated coefficients

(Intercept)     Latitude
0.0004775391 1.1955899446

 

exp(confint(model))             # 95% CI for exponentiated coefficients

                   2.5 %      97.5 %
(Intercept) 7.482379e-05 0.002822181
Latitude    1.148221e+00 1.247077992

 

Analysis of variance for individual terms

library(car)

Anova(model, type="II", test="Wald")

Analysis of Deviance Table (Type II tests)

Response: Trials
          Df  Chisq Pr(>Chisq)   
Latitude   1 72.076  < 2.2e-16 ***

Overall p-value for model

 

anova(model,
      update(model, ~1),    # update here produces null model for comparison
      test="Chisq")

Analysis of Deviance Table

Model 1: Trials ~ Latitude
Model 2: Trials ~ 1
  Resid. Df Resid. Dev Df Deviance  Pr(>Chi)   
1         6     70.333                         
2         7    153.633 -1  -83.301 < 2.2e-16 ***

 

library(lmtest)

lrtest(model)

Likelihood ratio test

Model 1: Trials ~ Latitude
Model 2: Trials ~ 1
  #Df  LogLik Df  Chisq Pr(>Chisq)   
1   2 -56.293                         
2   1 -97.944 -1 83.301  < 2.2e-16 ***

Pseudo r-squared

In order to calculate the pseudo r-squared for a logistic model, it’s necessary to convert the data to long format, and re-fit the model.  Here, I’ll re-type the data in a slightly longer format, and then use tidyr::uncount to convert the data frame to true long format, with 4444 observations.

Data = read.table(header=TRUE, stringsAsFactors=TRUE, text="
 Location           Latitude  Allele  Count
 Port_Townsend,_WA  48.1      mpi90      47
 Neskowin,_OR       45.2      mpi90     177
 Siuslaw_R.,_OR     44.0      mpi90    1087
 Umpqua_R.,_OR      43.7      mpi90     187
 Coos_Bay,_OR       43.5      mpi90     397
 San_Francisco,_CA  37.8      mpi90      40
 Carmel,_CA         36.6      mpi90      39
 Santa_Barbara,_CA  34.3      mpi90      30

Port_Townsend,_WA   48.1      mpi100    139
Neskowin,_OR        45.2      mpi100    241
Siuslaw_R.,_OR      44.0      mpi100   1183
Umpqua_R.,_OR       43.7      mpi100    175
Coos_Bay,_OR        43.5      mpi100    671
San_Francisco,_CA   37.8      mpi100     14
San_Francisco,_CA   36.6      mpi100     17
Santa_Barbara,_CA   34.3      mpi100      0
")

str(Data)
'data.frame': 16 obs. of  4 variables:
  $ Location: Factor w/ 8 levels "Carmel,_CA","Coos_Bay,_OR",..: 4 3 7 8 2 5 1 6 4 3 ...
$ Latitude: num  48.1 45.2 44 43.7 43.5 37.8 36.6 34.3 48.1 45.2 ...
$ Allele  : Factor w/ 2 levels "mpi100","mpi90": 2 2 2 2 2 2 2 2 1 1 ...
$ Count   : int  47 177 1087 187 397 40 39 30 139 241 ...

 

library(tidyr)

Long = uncount(Data, Count)

str(Long)

'data.frame': 4444 obs. of  3 variables:
  $ Location: Factor w/ 8 levels "Carmel,_CA","Coos_Bay,_OR",..: 4 4 4 4 4 4 4 4 4 4 ...
$ Latitude: num  48.1 48.1 48.1 48.1 48.1 48.1 48.1 48.1 48.1 48.1 ...
$ Allele  : Factor w/ 2 levels "mpi100","mpi90": 2 2 2 2 2 2 2 2 2 2 ...

 

model.2 = glm(Allele ~ Latitude, data = Long,
              family = binomial())

summary(model.2)

Coefficients:

             Estimate Std. Error z value Pr(>|z|)   
(Intercept)   7.64686    0.92487   8.268   <2e-16 ***
Latitude     -0.17864    0.02104  -8.490   <2e-16 ***

 

library(car)

Anova(model.2, test="Wald")

Analysis of Deviance Table (Type II tests)

         Df  Chisq Pr(>Chisq)   
Latitude  1 72.076  < 2.2e-16 ***

library(rcompanion)

nagelkerke(model.2)

$Pseudo.R.squared.for.model.vs.null

Pseudo.R.squared
McFadden                            0.0136160
Cox and Snell (ML)                  0.0185699
Nagelkerke (Cragg and Uhler)        0.0248401

$Likelihood.ratio.test

  Df.diff LogLik.diff  Chisq    p.value
-1      -41.65 83.301 7.0476e-20

library(rcompanion)

efronRSquared(model.2)

EfronRSquared
       0.0176

 

library(rcompanion)

countRSquare(model.2)

$Result

  Count.R2 Count.R2.corrected
1    0.567             0.0389

$Confusion.matrix

          Predicted

Actual       0    1  Sum
 0        2409   31 2440
 1        1895  109 2004
 Sum      4304  140 4444

Plot of standardized residuals

 

plot(fitted(model),
     rstandard(model))

 

 

A plot of standardized residuals vs. predicted values.  The residuals should be unbiased and homoscedastic.  For an illustration of these properties, see this diagram by Steve Jost at DePaul University: condor.depaul.edu/sjost/it223/documents/resid-plots.gif.

 

### additional model checking plots with: plot(model)

             

 

Plotting the model

 

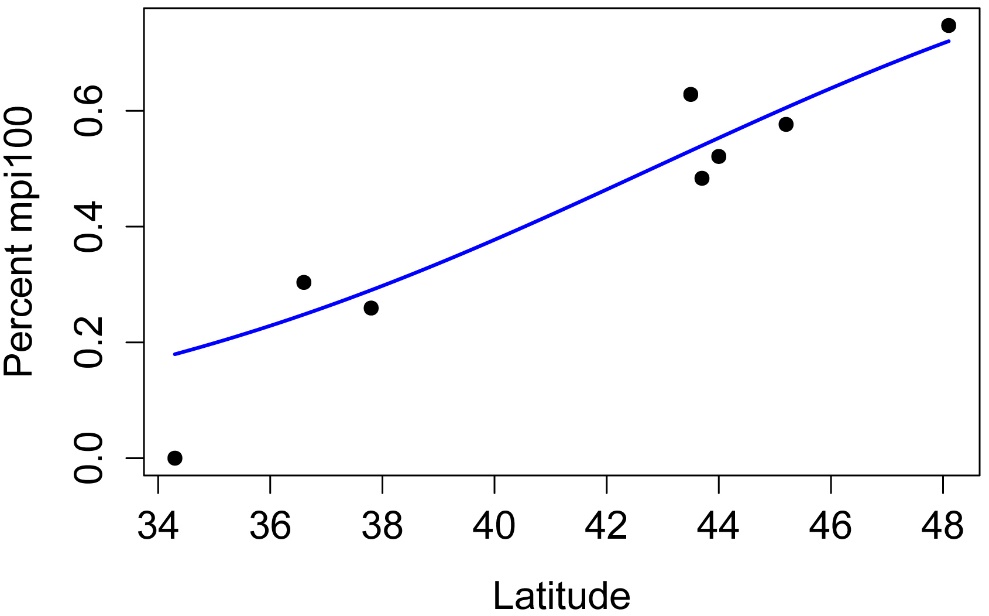
plot(Percent ~ Latitude,
     data = Data,
     xlab="Latitude",
     ylab="Percent mpi100",
     pch=19)             

curve(predict(model,data.frame(Latitude=x),type="response"),
      lty=1, lwd=2, col="blue",                           
      add=TRUE)

 

 

 

Logistic regression example

 

### --------------------------------------------------------------
### Logistic regression, favorite insect example, p. 248
### --------------------------------------------------------------

Data = read.table(header=TRUE, stringsAsFactors=TRUE, text="
Height  Insect                   
 62      beetle
 66      other
 61      beetle
 67      other
 62      other
 76      other
 66      other
 70      beetle
 67      other
 66      other
 70      other
 70      other
 77      beetle
 76      other
 72      beetle
 76      beetle
 72      other
 70      other
 65      other
 63      other
 63      other
 70      other
 72      other
 70      beetle
 74      other
")

 

Model fitting

 

model = glm(Insect ~ Height,
            data=Data,
            family = binomial(link="logit"))

 

 

Coefficients and exponentiated cofficients

 

summary(model)

 

Coefficients:

            Estimate Std. Error z value Pr(>|z|)

(Intercept)  4.41379    6.66190   0.663    0.508

Height      -0.05016    0.09577  -0.524    0.600

 

 

confint(model)

 

                 2.5 %     97.5 %

(Intercept) -8.4723648 18.4667731

Height      -0.2498133  0.1374819

 

exp(model$coefficients)         # exponentiated coefficients

 

(Intercept)      Height

 82.5821122   0.9510757

 

 

exp(confint(model))             # 95% CI for exponentiated coefficients

 

                   2.5 %       97.5 %

(Intercept) 0.0002091697 1.047171e+08

Height      0.7789461738 1.147381e+0

 

 

Analysis of variance for individual terms

 

library(car)

Anova(model, type="II", test="Wald")

Analysis of Deviance Table (Type II tests)

Response: Insect

          Df  Chisq Pr(>Chisq)
Height     1 0.2743     0.6004
Residuals 23

Overall p-value for model

 

anova(model,
      update(model, ~1),    # update here produces null model for comparison
      test="Chisq")

Analysis of Deviance Table

Model 1: Insect ~ Height
Model 2: Insect ~ 1
  Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1        23     29.370                    
2        24     29.648 -1 -0.27779   0.5982

library(lmtest)

lrtest(model)

Likelihood ratio test

Model 1: Insect ~ Height
Model 2: Insect ~ 1
  #Df  LogLik Df  Chisq Pr(>Chisq)
1   2 -14.685                    
2   1 -14.824 -1 0.2778     0.5982

Pseudo-R-squared

 

library(rcompanion)

nagelkerke(model)

$Pseudo.R.squared.for.model.vs.null
                             Pseudo.R.squared
McFadden                           0.00936978
Cox and Snell (ML)                 0.01105020
Nagelkerke (Cragg and Uhler)       0.01591030

library(rcompanion)

efronRSquared(model)

 

EfronRSquared

       0.0147

library(rcompanion)

countRSquare(model)

$Result
  Count.R2 Count.R2.corrected
1     0.72                  0

Plot of standardized residuals

 

plot(fitted(model),
     rstandard(model))

 

 

 

Plotting the model

 

###  Convert Insect to a numeric variable, levels 0 and 1

Data$Insect.num=as.numeric(Data$Insect)-1

library(FSA)

headtail(Data)

 

   Height Insect Insect.num

1      62 beetle          0

2      66  other          1

3      61 beetle          0

23     72  other          1

24     70 beetle          0

25     74  other          1

plot(Insect.num ~ Height,
     data = Data,
     xlab="Height",
     ylab="Insect",
     pch=19)             

curve(predict(model,data.frame(Height=x),type="response"),
      lty=1, lwd=2, col="blue",                           
      add=TRUE)

 

 

 

###  Convert Insect to a logical variable, levels TRUE and FALSE

Data$Insect.log=(Data$Insect=="other")

library(FSA)

headtail(Data)

 

   Height Insect Insect.num Insect.log

1      62 beetle          0      FALSE

2      66  other          1       TRUE

3      61 beetle          0      FALSE

23     72  other          1       TRUE

24     70 beetle          0      FALSE

25     74  other          1       TRUE

 

 

library(popbio)

logi.hist.plot(Data$Height,
               Data$Insect.log,
               boxp=FALSE,
               type="hist",
               col="gray",
               xlabel="Height")

 

 

 

Logistic regression example with significant model and abbreviated code

 

### --------------------------------------------------------------
### Logistic regression, hypothetical example
### Abbreviated code and description
### --------------------------------------------------------------

Data = read.table(header=TRUE, stringsAsFactors=TRUE, text="
Continuous  Factor
 62          A
 63          A
 64          A
 65          A
 66          A
 67          A
 68          A
 69          A
 70          A
 71          A
 72          A
 73          A
 74          A
 75          A
 72.5        B     
 73.5        B     
 74.5        B
 75          B     
 76          B
 77          B     
 78          B
 79          B     
 80          B
 81          B     
 82          B
 83          B     
 84          B
 85          B     
 86          B
")


model = glm(Factor ~ Continuous,
            data=Data,
            family = binomial(link="logit"))


summary(model)

 

Coefficients:
            Estimate Std. Error z value Pr(>|z|) 
(Intercept) -66.4981    32.3787  -2.054   0.0400 *
Continuous    0.9027     0.4389   2.056   0.0397 *

library(car)

Anova(model, type="II", test="Wald")

 

Analysis of Deviance Table (Type II tests)

Response: Factor
           Df Chisq Pr(>Chisq) 
Continuous  1 4.229    0.03974 *
Residuals  27                  

anova(model,
      update(model, ~1),
      test="Chisq")

 

  Resid. Df Resid. Dev Df Deviance Pr(>Chi)   
1        27     12.148                        
2        28     40.168 -1   -28.02  1.2e-07 ***

library(rcompanion)

nagelkerke(model)

                             Pseudo.R.squared
McFadden                             0.697579
Cox and Snell (ML)                   0.619482
Nagelkerke (Cragg and Uhler)         0.826303

library(rcompanion)

efronRSquared(model)

EfronRSquared
         0.71

library(rcompanion)

countRSquare(model)

$Result

  Count.R2 Count.R2.corrected
1    0.862              0.714

$Confusion.matrix

   Predicted
Actual  0  1 Sum
   0   12  2  14
   1    2 13  15
   Sum 14 15  29

 

plot(fitted(model),
     rstandard(model))

 

 

###  Convert Factor to a numeric variable, levels 0 and 1

Data$Factor.num=as.numeric(Data$Factor)-1

library(FSA)

headtail(Data)

 

   Continuous Factor Factor.num

1          62      A          0

2          63      A          0

3          64      A          0

27         84      B          1

28         85      B          1

29         86      B          1

 

 

plot(Factor.num  ~ Continuous,
     data = Data,
     xlab="Continuous",
     ylab="Factor",
     pch=19)             

curve(predict(model,data.frame(Continuous=x),type="response"),
      lty=1, lwd=2, col="blue",                           
      add=TRUE)

 

 

 

###  Convert Factor to a logical variable, levels TRUE and FALSE

Data$Factor.log=(Data$Factor=="B")

library(FSA)

headtail(Data)

 

   Continuous Factor Factor.num Factor.log

1          62      A          0      FALSE

2          63      A          0      FALSE

3          64      A          0      FALSE

27         84      B          1       TRUE

28         85      B          1       TRUE

29         86      B          1       TRUE

 

 

library(popbio)

logi.hist.plot(Data$Continuous,
               Data$Factor.log,
               boxp=FALSE,
               type="hist",
               col="gray",
               xlabel="Height")

 

 

 

Power analysis

 

See the Handbook for information on this topic.

 

References

 

IDRE . 2011. FAQ: What are pseudo R-squareds? UCLA. stats.oarc.ucla.edu/other/mult-pkg/faq/general/faq-what-are-pseudo-r-squareds/.

 

Cross Validated. 2014. McFadden's Pseudo-R2 Interpretation. stats.stackexchange.com/questions/82105/mcfaddens-pseudo-r2-interpretation.

 

©2015 by Salvatore S. Mangiafico.
Rutgers Cooperative Extension, New Brunswick, NJ.

Organization of statistical tests and selection of examples for these tests ©2014 by John H. McDonald.  Used with permission.

Non-commercial reproduction of this content, with attribution, is permitted.  For-profit reproduction without permission is prohibited.

If you use the code or information in this site in a published work, please cite it as a source.  Also, if you are an instructor and use this book in your course, please let me know.   My contact information is on the About the Author page.

Citation:

Mangiafico, S.S. 2015. An R Companion for the Handbook of Biological Statistics, version 1.3.9, revised 2023.
rcompanion.org/rcompanion/. (Pdf version: rcompanion.org/documents/RCompanionBioStatistics.pdf.)