Paired t-tests can be conducted with the t.test function in the native stats package using the paired=TRUE option. Data can be in long format or short format. Examples of each are shown in this chapter.
As a non-parametric alternative to paired t-tests, a permutation test can be used. An example is shown in the “Permutation test for dependent samples” section of this chapter.
Examples in Summary and Analysis of Extension Program Evaluation
SAEPER: One-way Permutation Test of Symmetry for Paired Ordinal Data
Packages used in this chapter
The following commands will install these packages if they are not already installed:
if(!require(ggplot2)){install.packages("ggplot2")}
if(!require(coin)){install.packages("coin")}
if(!require(pwr)){install.packages("pwr")}
When to use it
The horseshoe crab example is shown at the end of the “How to do the test” section.
Null hypothesis
Assumption
How the test works
See the Handbook for information on these topics.
Examples
The flicker feather example is shown in the “How to do the test” section.
Graphing the results
Plots are shown in the “How to do the test” section.
How to do the test
Paired t-test, data in wide format, flicker feather example
###
--------------------------------------------------------------
### Paired t-test, Flicker feather example, p. 185
### --------------------------------------------------------------
Input = ("
Bird Typical Odd
A -0.255 -0.324
B -0.213 -0.185
C -0.190 -0.299
D -0.185 -0.144
E -0.045 -0.027
F -0.025 -0.039
G -0.015 -0.264
H 0.003 -0.077
I 0.015 -0.017
J 0.020 -0.169
K 0.023 -0.096
L 0.040 -0.330
M 0.040 -0.346
N 0.050 -0.191
O 0.055 -0.128
P 0.058 -0.182
")
Data = read.table(textConnection(Input),header=TRUE)
Paired t-test
t.test(Data$Typical,
Data$Odd,
paired=TRUE,
conf.level=0.95)
t = 4.0647, df = 15, p-value = 0.001017
mean of the differences
0.137125
Simple plot of differences
Difference = Data$Odd - Data$Typical
plot(Difference,
pch = 16,
ylab="Difference (Odd – Typical)")
abline(0,0, col="blue", lwd=2)

A simple plot of differences between one sample and the other. Points below the blue line indicate observations where Typical is greater than Odd, that is where (Odd – Typical) is negative.
Simple 1-to-1 plot of values
plot(Data$Typical, Data$Odd,
pch = 16,
xlab="Typical feathers",
ylab="Odd feathers")
abline(0,1, col="blue", lwd=2)
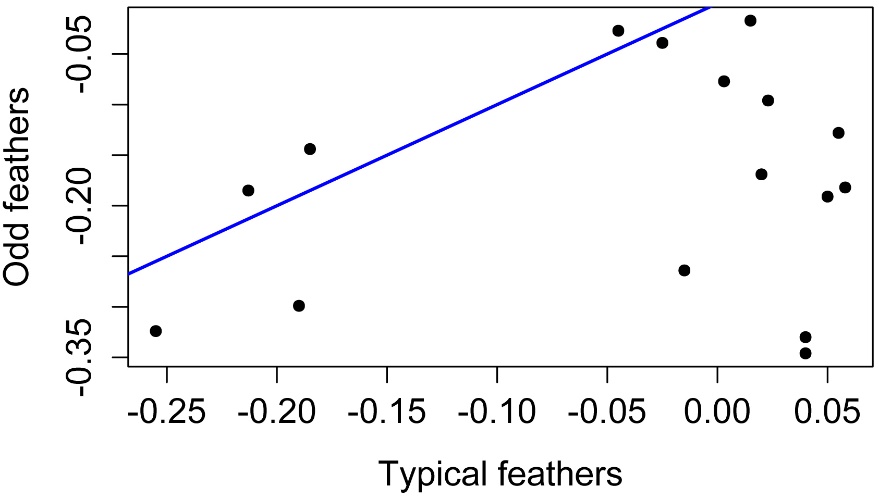
Plot of paired samples from a paired t-test. Circles below or to the right of the blue one-to-one line indicate observations with a higher value for Typical than for Odd.
Checking assumptions of the model
Difference = Data$Odd - Data$Typical
hist(Difference,
col="gray",
main="Histogram of differences",
xlab="Difference")

Histogram of differences of two populations from a paired t-test. Distribution of differences should be approximately normal. Bins with negative values indicate observations with a higher value for Typical than for Odd.
Graphing the results
Data$Difference = Data$Odd - Data$Typical
library(ggplot2)
ggplot(Data,
aes(x = Bird,
y = Difference)) +
geom_bar(stat = "identity",
fill = "grey50",
colour = "black",
width = 0.6) +
scale_y_continuous(breaks = seq(-0.4, 0.1, 0.1),
limits = c(-0.4, 0.1),
expand = c(0, 0)) +
#ggtitle("Chart title") +
labs(x = "Bird identification letter",
y = "Difference in yellowness index (Typical – Odd)") +
theme_bw() +
theme(panel.grid.major.x = element_blank(),
panel.grid.major.y = element_line(colour = "grey50"),
plot.title = element_text(size = rel(1.5),
face = "bold", vjust = 1.5),
axis.ticks.x = element_blank(),
axis.ticks.y = element_blank(),
axis.title.y = element_text(face = "bold",
vjust= 1.8),
axis.title.x = element_text(face = "bold",
vjust= -0.8)
)
# # #

Paired t-test, data in wide format, horseshoe crab example
###
--------------------------------------------------------------
### Paired t-test, Horseshoe crab example, pp. 181–182
### --------------------------------------------------------------
# Note, if you use "2011" as a variable name,
# the read.table function will convert it to "X2011"
Input = ("
Beach Year.2011 Year.2012
'Bennetts Pier' 35282 21814
'Big Stone' 359350 83500
'Broadkill' 45705 13290
'Cape Henlopen' 49005 30150
'Fortescue' 68978 125190
'Fowler' 8700 4620
'Gandys' 18780 88926
'Higbees' 13622 1205
'Highs' 24936 29800
'Kimbles' 17620 53640
'Kitts Hummock' 117360 68400
'Norburys Landing' 102425 74552
'North Bowers' 59566 36790
'North Cape May' 32610 4350
'Pickering' 137250 110550
'Pierces Point' 38003 43435
'Primehook' 101300 20580
'Reeds' 62179 81503
'Slaughter' 203070 53940
'South Bowers' 135309 87055
'South CSL' 150656 112266
'Ted Harvey' 115090 90670
'Townbank' 44022 21942
'Villas' 56260 32140
'Woodland' 125 1260
")
Data = read.table(textConnection(Input),header=TRUE)
Paired t-test
t.test(Data$Year.2011, Data$Year.2012,
paired=TRUE,
conf.level=0.95)
t = 2.1119, df = 24, p-value = 0.04529
mean of the differences
28225.4
Simple 1-to-1 plot of values
plot(Data$Year.2011, Data$Year.2012,
pch = 16,
xlab="2011",
ylab="2012")
abline(0,1, col="blue", lwd=2)

Plot of paired samples from a paired t-test. Circles below and to the right of the blue one-to-one line indicate observations with a higher value for 2011 than for 2012.
Difference = Data$Year.2012 - Data$Year.2011
hist(Difference,
col="gray",
main="Histogram of differences",
xlab="Difference")

Histogram of differences in two populations from paired t-test. Distribution of differences should be approximately normal. Bins with negative values indicate observations with a higher score for 2011 than for 2012.
# # #
Paired t-test, data in long format
###
--------------------------------------------------------------
### Paired t-test, long format data, Flicker feather example, p. 185
### --------------------------------------------------------------
Input = ("
Bird Feather Length
A Typical -0.255
B Typical -0.213
C Typical -0.19
D Typical -0.185
E Typical -0.045
F Typical -0.025
G Typical -0.015
H Typical 0.003
I Typical 0.015
J Typical 0.02
K Typical 0.023
L Typical 0.04
M Typical 0.04
N Typical 0.05
O Typical 0.055
P Typical 0.058
A Odd -0.324
B Odd -0.185
C Odd -0.299
D Odd -0.144
E Odd -0.027
F Odd -0.039
G Odd -0.264
H Odd -0.077
I Odd -0.017
J Odd -0.169
K Odd -0.096
L Odd -0.33
M Odd -0.346
N Odd -0.191
O Odd -0.128
P Odd -0.182
")
Data = read.table(textConnection(Input),header=TRUE)
### Note: data must be ordered so that the
first observation of Group 1
### is the same subject as the first observation of Group 2
Unfortunately, R now makes you extract the two vectors of data from the data frame for the paired test.
Typical = Data$Length[Data$Feather=="Typical"]
Odd = Data$Length[Data$Feather=="Odd"]
t.test(Typical, Odd,
paired=TRUE,
conf.level=0.95)
t = 4.0647, df = 15, p-value = 0.001017
mean of the differences
-0.137125
# # #
Permutation test for dependent samples
This permutation test is analogous to a paired t-test.
###
--------------------------------------------------------------
### Paired two-sample permutation test, long format data
### Flicker feather example, p. 185
### --------------------------------------------------------------
Input = ("
Bird Feather Length
A Typical -0.255
B Typical -0.213
C Typical -0.19
D Typical -0.185
E Typical -0.045
F Typical -0.025
G Typical -0.015
H Typical 0.003
I Typical 0.015
J Typical 0.02
K Typical 0.023
L Typical 0.04
M Typical 0.04
N Typical 0.05
O Typical 0.055
P Typical 0.058
A Odd -0.324
B Odd -0.185
C Odd -0.299
D Odd -0.144
E Odd -0.027
F Odd -0.039
G Odd -0.264
H Odd -0.077
I Odd -0.017
J Odd -0.169
K Odd -0.096
L Odd -0.33
M Odd -0.346
N Odd -0.191
O Odd -0.128
P Odd -0.182
")
Data = read.table(textConnection(Input),header=TRUE)
library(coin)
independence_test(Length ~ Feather | Bird,
data = Data)
Asymptotic General Independence Test
Z = -2.8959, p-value = 0.003781
# # #
Power analysis
Power analysis for paired t-test
###
--------------------------------------------------------------
### Power analysis, paired t-test, pp. 185–186
### --------------------------------------------------------------
Detect = 0.1 # Difference in
means to detect
SD = 0.135 # Standard
deviation of differences
Cohen.d = Detect/SD
library(pwr)
pwr.t.test(
n = NULL, # Number of
_pairs_ of observations
d = Cohen.d,
sig.level = 0.05, # Type I
probability
power = 0.90, # 1 minus Type
II probability
type = "paired", #
paired t-test
alternative = "two.sided")
Paired t test power calculation
n = 21.16434
NOTE: n is number of *pairs*
# # #
![Batsto Lake, Wharton State Forest, New Jersey [banner]](images/banner.png)