An R Companion for the Handbook of Biological Statistics

Salvatore S. Mangiafico

Chi-square Test of Goodness-of-Fit

Examples in Summary and Analysis of Extension Program Evaluation

SAEPER: Goodness-of-Fit Tests for Nominal Variables

 

Packages used in this chapter

The following commands will install these packages if they are not already installed:

if(!require(dplyr)){install.packages("dplyr")}
if(!require(ggplot2)){install.packages("ggplot2")}
if(!require(grid)){install.packages("grid")}
if(!require(pwr)){install.packages("pwr")}

 

When to use it

Null hypothesis

See the Handbook for information on these topics.

 

How the test works

Chi-square goodness-of-fit example

 

### --------------------------------------------------------------
### Drosophila example, Chi-square goodness-of-fit, p. 46
### --------------------------------------------------------------

observed = c(770, 230)        # observed frequencies
expected = c(0.75, 0.25)      # expected proportions

chisq.test(x = observed,
           p = expected)

 

X-squared = 2.1333, df = 1, p-value = 0.1441

 

#     #     #

 

 

Post-hoc test

Assumptions

See the Handbook for information on these topics.

 

Examples: extrinsic hypothesis

 

### --------------------------------------------------------------
### Crossbill example, Chi-square goodness-of-fit, p. 47
### --------------------------------------------------------------

observed = c(1752, 1895)    # observed frequencies
expected = c(0.5, 0.5)      # expected proportions

chisq.test(x = observed,
           p = expected)

 

X-squared = 5.6071, df = 1, p-value = 0.01789

 

#     #     #

 

 

### --------------------------------------------------------------
### Rice example, Chi-square goodness-of-fit, p. 47
### --------------------------------------------------------------

observed = c(772, 1611, 737)
expected = c(0.25, 0.50, 0.25)

chisq.test(x = observed,
           p = expected)

 

X-squared = 4.1199, df = 2, p-value = 0.1275

 

#     #     #

 

 

### --------------------------------------------------------------
### Bird foraging example, Chi-square goodness-of-fit, pp. 47–48
### --------------------------------------------------------------

observed = c(70, 79, 3, 4)
expected = c(0.54, 0.40, 0.05, 0.01)

chisq.test(x = observed,
           p = expected)

  

X-squared = 13.5934, df = 3, p-value = 0.0035

 

#     #     #

 

 

Example: intrinsic hypothesis  

 

### --------------------------------------------------------------
### Intrinsic example, Chi-square goodness-of-fit, p. 48
### --------------------------------------------------------------

observed       = c(1203,  2919,  1678)
expected.prop  = c(0.211, 0.497, 0.293)

expected.count = sum(observed)*expected.prop

chi2 = sum((observed- expected.count)^2/ expected.count)

chi2

 

[1] 1.082646

 

pchisq(chi2,
       df=1,
       lower.tail=FALSE)   

  

[1] 0.2981064

 

#     #     #

 

 

Graphing the results

The first example below will use the barplot function in the native graphics package to produce a simple plot.  First we will calculate the observed proportions and then copy those results into a matrix format for plotting.  We’ll call this matrix Matriz.  See the “Chi-square Test of Independence” section for a few notes on creating matrices. 

 

The second example uses the package ggplot2, and uses a data frame instead of a matrix.  The data frame is named Forage.  For this example, the code calculates confidence intervals and adds them to the data frame.  This code could be skipped if those values were determined manually and put into a data frame from which the plot could be generated.

 

Sometimes factors will need to have the order of their levels specified for ggplot2 to put them in the correct order on the plot, as in the second example.  Otherwise R will alphabetize levels.

 

Simple bar plot with barplot

 

### --------------------------------------------------------------
### Simple bar plot of proportions, p. 49
###      Uses data in a matrix format
### --------------------------------------------------------------

observed = c(70, 79, 3, 4)

expected = c(0.54, 0.40, 0.05, 0.01)

total = sum(observed)

observed.prop = observed / total

observed.prop

 

[1] 0.44871795 0.50641026 0.01923077 0.02564103

 

 

### Re-enter data as a matrix

Input =("
Value     Douglas.fir  Ponderosa.pine  Grand.fir   Western.larch
Observed  0.4487179    0.5064103       0.01923077  0.02564103
Expected  0.5400000    0.4000000       0.05000000  0.01000000  
")

Matriz = as.matrix(read.table(textConnection(Input),
                   header=TRUE,
                   row.names=1))

Matriz

 

         Douglas fir Ponderosa pine  Grand fir Western larch

Observed   0.4487179      0.5064103 0.01923077    0.02564103

Expected   0.5400000      0.4000000 0.05000000    0.01000000

 

 

barplot(Matriz,
        beside=TRUE,
        legend=TRUE,
        ylim=c(0, 0.6),
        xlab="Tree species",
        ylab="Foraging proportion")

 

#     #     #

 

 

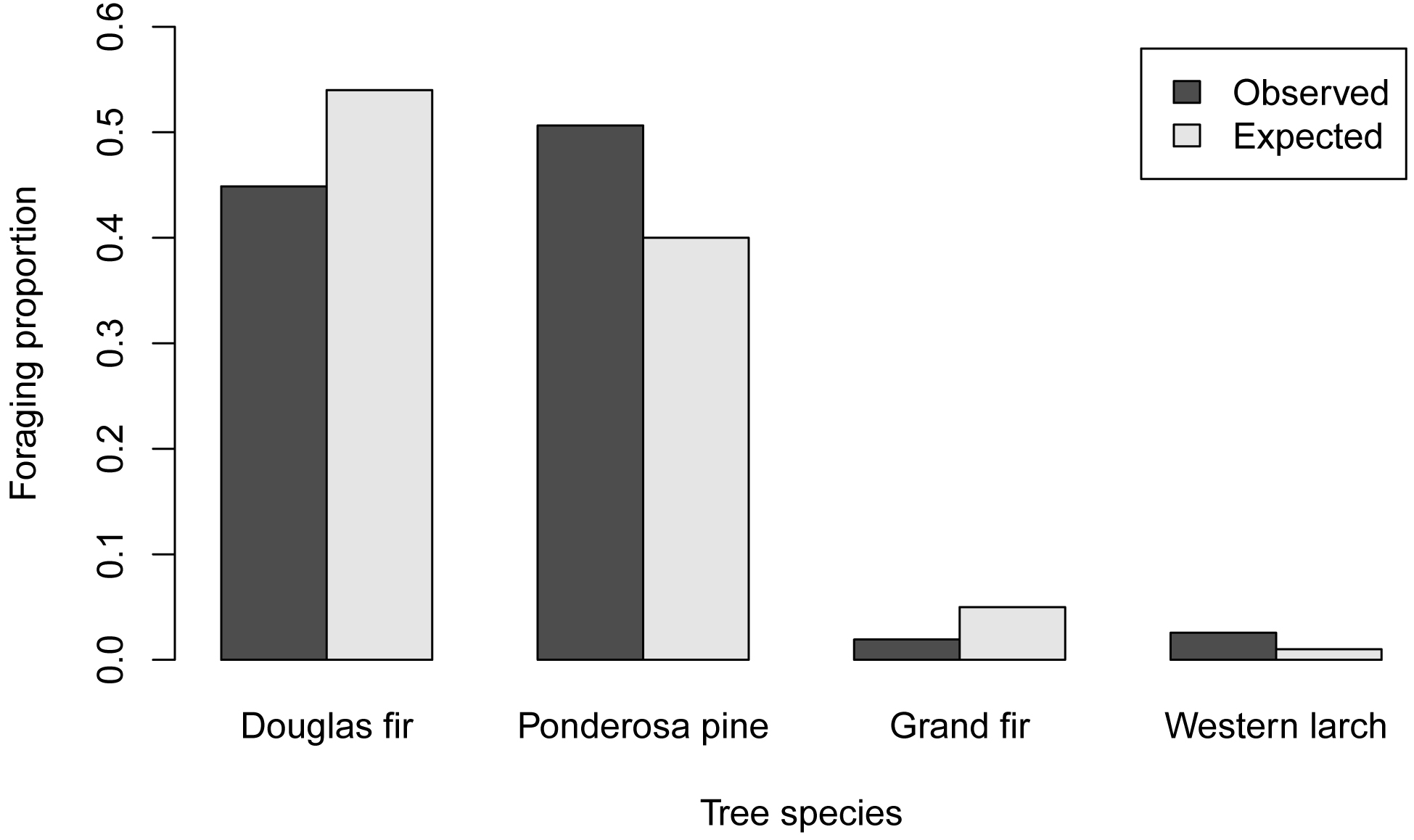
Bar plot with confidence intervals with ggplot2

The plot below is a bar char with confidence intervals.  The code calculates confidence intervals.  This code could be skipped if those values were determined manually and put in to a data frame from which the plot could be generated.

 

Sometimes factors will need to have the order of their levels specified for ggplot2 to put them in the correct order on the plot.  Otherwise R will alphabetize levels.

 

### --------------------------------------------------------------
### Graph example, Chi-square goodness-of-fit, p. 49
###    Using ggplot2
###    Plot adapted from:
###       shinyapps.stat.ubc.ca/r-graph-catalog/  
### --------------------------------------------------------------

Input =("
Tree              Value      Count   Total Proportion  Expected
'Douglas fir'     Observed   70      156   0.4487      0.54
'Douglas fir'     Expected   54      100   0.54        0.54
'Ponderosa pine'  Observed   79      156   0.5064      0.40
'Ponderosa pine'  Expected   40      100   0.40        0.40
'Grand fir'       Observed    3      156   0.0192      0.05
'Grand fir'       Expected    5      100   0.05        0.05
'Western larch'   Observed    4      156   0.0256      0.01
'Western larch'   Expected    1      100   0.01        0.01
")
 
Forage = read.table(textConnection(Input),header=TRUE)


### Specify the order of factor levels. Otherwise R will alphabetize them.

library(dplyr)

Forage =
mutate(Forage,
       Tree = factor(Tree, levels=unique(Tree)),
       Value = factor(Value, levels=unique(Value))
       )
      

### Add confidence intervals

Forage =
mutate(Forage,      
       low.ci = apply(Forage[c("Count", "Total", "Expected")],
                       1,
                       function(x)
                       binom.test(x["Count"], x["Total"], x["Expected"]
                                 )$ conf.int[1]),
                                
        upper.ci = apply(Forage[c("Count", "Total", "Expected")],
                         1,
                         function(x)
                         binom.test(x["Count"], x["Total"], x["Expected"]
                                    )$ conf.int[2])
         )

Forage$ low.ci [Forage$ Value == "Expected"] = 0
Forage$ upper.ci [Forage$ Value == "Expected"] = 0

Forage

 

            Tree    Value Count Total Proportion Expected      low.ci   upper.ci

1    Douglas fir Observed    70   156     0.4487     0.54 0.369115906 0.53030534

2    Douglas fir Expected    54   100     0.5400     0.54 0.000000000 0.00000000

3 Ponderosa pine Observed    79   156     0.5064     0.40 0.425290653 0.58728175

4 Ponderosa pine Expected    40   100     0.4000     0.40 0.000000000 0.00000000

5      Grand fir Observed     3   156     0.0192     0.05 0.003983542 0.05516994

6      Grand fir Expected     5   100     0.0500     0.05 0.000000000 0.00000000

7  Western larch Observed     4   156     0.0256     0.01 0.007029546 0.06434776

8  Western larch Expected     1   100     0.0100     0.01 0.000000000 0.00000000

 

 

### Plot adapted from:
###   shinyapps.stat.ubc.ca/r-graph-catalog/
 
library(ggplot2)
library(grid)

ggplot(Forage,
   aes(x = Tree, y = Proportion, fill = Value,
       ymax=upper.ci, ymin=low.ci))  +
       geom_bar(stat="identity", position = "dodge", width = 0.7) +
       geom_bar(stat="identity", position = "dodge",
                colour = "black", width = 0.7,
                show_guide = FALSE)  +
       scale_y_continuous(breaks = seq(0, 0.60, 0.1),
                limits = c(0, 0.60),
                expand = c(0, 0))  +
       scale_fill_manual(name = "Count type" ,
                 values = c('grey80', 'grey30'),
                 labels = c("Observed value",
                            "Expected value"))  +
       geom_errorbar(position=position_dodge(width=0.7),
                     width=0.0, size=0.5, color="black")  +
       labs(x = "Tree species",
            y = "Foraging proportion")  +
       ## ggtitle("Main title") +
       theme_bw()  +
       theme(panel.grid.major.x = element_blank(),
             panel.grid.major.y = element_line(colour = "grey50"),
             plot.title = element_text(size = rel(1.5),
             face = "bold", vjust = 1.5),
             axis.title = element_text(face = "bold"),
             legend.position = "top",
             legend.title = element_blank(),
             legend.key.size = unit(0.4, "cm"),
             legend.key = element_rect(fill = "black"),
             axis.title.y = element_text(vjust= 1.8),
             axis.title.x = element_text(vjust= -0.5)
            )

 

#     #     #

 

Bar plot of proportions vs. categories.  Error bars indicate 95% confidence intervals for each observed proportion.

 

 

Similar tests

Chi-square vs. G–test

See the Handbook for information on these topics.  The exact test of goodness-of-fit, the G-test of goodness-of-fit, and the exact test of goodness-of-fit tests are described elsewhere in this book.

 

How to do the test

Chi-square goodness-of-fit example

### --------------------------------------------------------------
### Pea color example, Chi-square goodness-of-fit, pp. 50–51
### --------------------------------------------------------------

observed = c(423, 133)  
expected = c(0.75, 0.25)
 
chisq.test(x = observed,
           p = expected)

 

X-squared = 0.3453, df = 1, p-value = 0.5568

 

#     #     #

 

 

Power analysis

Power analysis for chi-square goodness-of-fit

 

### --------------------------------------------------------------
### Power analysis, Chi-square goodness-of-fit, snapdragons, p. 51
### --------------------------------------------------------------

library(pwr)

P0      = c(0.25,  0.50, 0.25)
P1      = c(0.225, 0.55, 0.225)

effect.size = ES.w1(P0, P1) 

degrees = length(P0) - 1

pwr.chisq.test(
               w=effect.size,
               N=NULL,            # Total number of observations
               df=degrees,
               power=0.80,        # 1 minus Type II probability
               sig.level=0.05)    # Type I probability

 

N = 963.4689

 

#     #     #

 

©2015 by Salvatore S. Mangiafico.
Rutgers Cooperative Extension, New Brunswick, NJ.

Organization of statistical tests and selection of examples for these tests ©2014 by John H. McDonald.  Used with permission.

Non-commercial reproduction of this content, with attribution, is permitted.  For-profit reproduction without permission is prohibited.

If you use the code or information in this site in a published work, please cite it as a source.  Also, if you are an instructor and use this book in your course, please let me know.   My contact information is on the About the Author page.

Citation:

Mangiafico, S.S. 2015. An R Companion for the Handbook of Biological Statistics, version 1.3.9, revised 2023.
rcompanion.org/rcompanion/. (Pdf version: rcompanion.org/documents/RCompanionBioStatistics.pdf.)