Python Handbook: Mann-Whitney Test

Two-sample Mann–Whitney test in SAEPER

For a discussion of this test, see the corresponding chapter in Summary and Analysis of Extension Program Evaluation in R (rcompanion.org/handbook/F_04.html).

Importing packages in this chapter

The following commands will import required packages used in this chapter from libraries and assign them common aliases. You may need install these libraries first.

import io

import os

import numpy as np

import scipy.stats as stats

import pandas as pd

import matplotlib.pyplot as plt

import pingouin as pg

import seaborn as sns

Setting your working directory

You may wish to set your working directory for exported plots.

os.chdir("C:/Users/Sal Mangiafico/Desktop")

print(os.getcwd())

Example of Mann–Whitney test

Data = pd.read_table(sep="\\s+", filepath_or_buffer=io.StringIO("""
Speaker Likert
Pooh      3
Pooh      5
Pooh      4
Pooh      4
Pooh      4
Pooh      4
Pooh      4
Pooh      4
Pooh      5
Pooh      5
Piglet    2
Piglet    4
Piglet    2
Piglet    2
Piglet    1
Piglet    2
Piglet    3
Piglet    2
Piglet    2
Piglet    3
"""))

### Convert Speaker to category type

Data['Speaker'] = Data['Speaker'].astype('category')

### Create new variable, Likert as a category variable

Data['Likert.f'] = Data['Likert'].astype('category')

### Order Speaker by desired values

SpeakerLevels = ["Pooh", "Piglet"]

Data['Speaker'] = Data['Speaker'].cat.reorder_categories(SpeakerLevels)

### Display some summary statistics for the data frame

print(Data.info())

Data columns (total 3 columns):

# Column Non-Null Count Dtype

--- ------ -------------- -----

0 Speaker 20 non-null category

1 Likert 20 non-null int64

2 Likert.f 20 non-null category

print(Data['Speaker'].cat.categories)

Index(['Pooh', 'Piglet'], dtype='object')

print(Data['Likert.f'].cat.categories)

Index([1, 2, 3, 4, 5], dtype='int64')

Summarize data treating Likert scores as factors

Note that the variable we want to count is Likert.f, which is a category variable. Counts for Likert.f are tabulated over values of Speaker. The normalize=True option reports proportions. If sort=True, the results will be ordered by which categories have the most observations.

Data['Likert.f'].value_counts(sort=False)

Likert.f

1 1

2 6

3 3

4 7

5 3

Name: count, dtype: int64

Data['Likert.f'].value_counts(sort=False, normalize=True)

Likert.f

1 0.05

2 0.30

3 0.15

4 0.35

5 0.15

Name: proportion, dtype: float64

Bar plot

Simple seaborn call

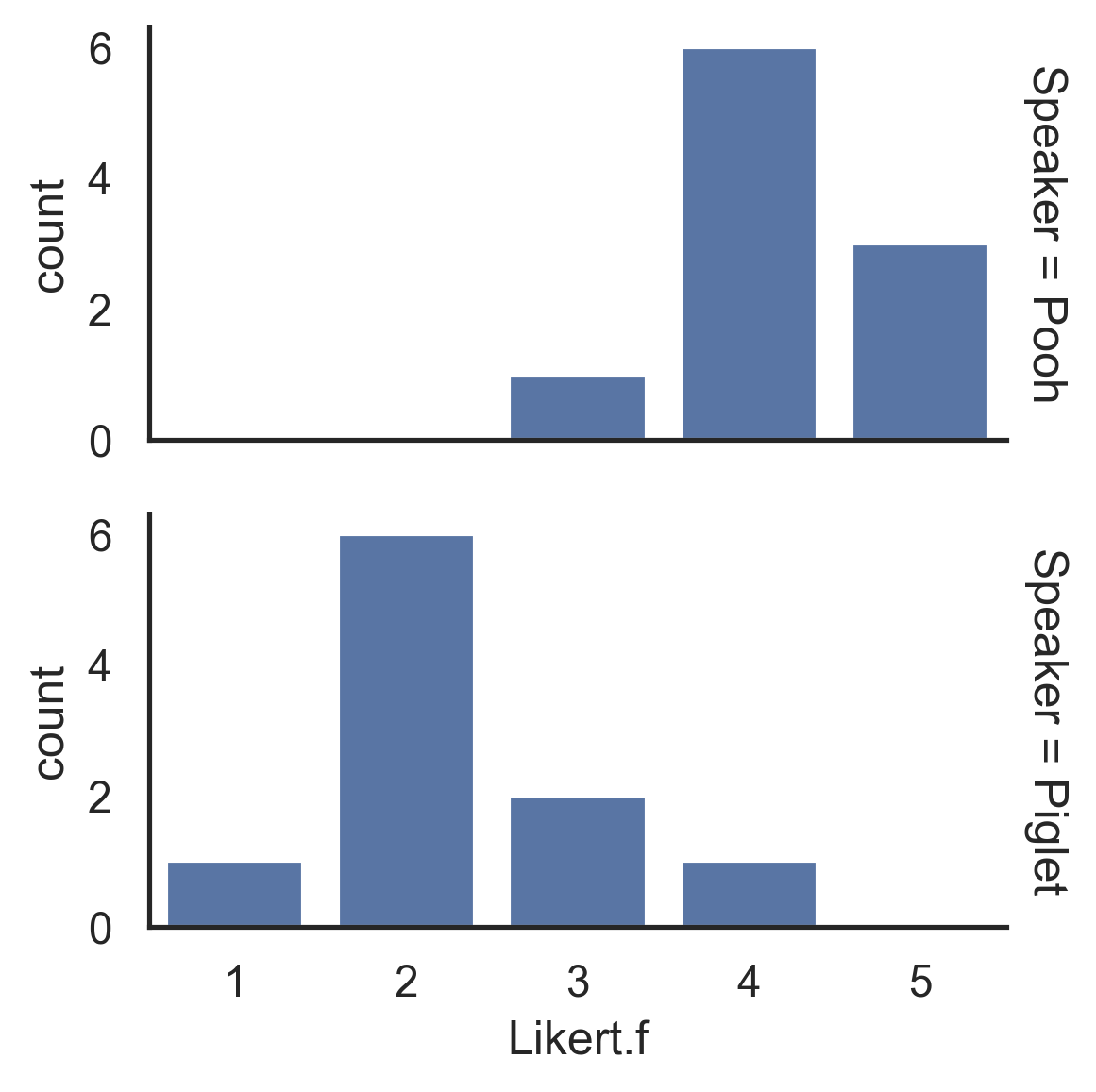
Plot = sns.FacetGrid(data=Data, row='Speaker',

margin_titles=True, height=2, aspect= 2)

Plot.map(sns.countplot, 'Likert.f')

Formatting and export as file

sns.set_theme(style='white')

Plot = sns.FacetGrid(data=Data, row='Speaker',

margin_titles=True, height=2, aspect= 2)

Plot.map(sns.countplot, 'Likert.f')

Plot.tight_layout()

Plot.savefig('CountPoohPiglet.png', format='png', dpi=300)

Histogram of bootstrapped means

Summarize data treating Likert scores as numeric

Summary = Data.groupby('Speaker')['Likert'].describe()

print(Summary)

count mean std min 25% 50% 75% max

Speaker

Pooh 10.0 4.2 0.632456 3.0 4.0 4.0 4.75 5.0

Piglet 10.0 2.3 0.823273 1.0 2.0 2.0 2.75 4.0

Wilcoxon–Mann–Whitney test

Using pingouin

To perform this test, we first need to extract the data as arrays of numbers. Here we’ll treat Piglet as the first group to match the R output.

Pooh = Data['Likert'][Data['Speaker']=='Pooh']

Piglet = Data['Likert'][Data['Speaker']=='Piglet']

pg.mwu(Piglet, Pooh)

U-val alternative p-val RBC CLES

MWU 5.0 two-sided 0.000471 -0.9 0.05

### Note that the output includes the rank biserial correlation coefficient, RBC, and

### the common languange effect size statistic, CLES, as effect size statistics.

Using scipy.stats