The two-sample Mann–Whitney U test is a rank-based test that compares values for two groups. A significant result suggests that the values for the two groups are different. It is equivalent to a two-sample Wilcoxon rank-sum test.
Without further assumptions about the distribution of the data, the Mann–Whitney test does not address hypotheses about the medians of the groups. Instead, the test addresses if it is likely that an observation in one group is greater than an observation in the other. This is sometimes stated as testing if one sample has stochastic dominance compared with the other.
The test assumes that the observations are independent. That is, it is not appropriate for paired observations or repeated measures data.
The test is performed with the wilcox.test function in the native stats package.
Appropriate effect size statistics include Vargha and Delaney’s A, Cliff’s delta, and the Glass rank biserial coefficient.
Appropriate data
• Two-sample data. That is, one-way data with two groups only
• Dependent variable is ordinal, interval, or ratio
• Independent variable is a factor with two levels. That is, two groups
• Observations between groups are independent. That is, not paired or repeated measures data
• In order to be a test of medians, the distributions of values for each group need to be of similar shape and spread. Otherwise, the test is typically a test of stochastic equality.
Hypotheses
• Null hypothesis: The two groups are sampled from populations with identical distributions. Typically, that the sampled populations exhibit stochastic equality.
• Alternative hypothesis (two-sided): The two groups are sampled from populations with different distributions. Typically, that one sampled population exhibits stochastic dominance.
Interpretation
Significant results can be reported as e.g. “Values for group A were significantly different from those for group B.”
Other notes and alternative tests
The Mann–Whitney U test can be considered equivalent to the Kruskal–Wallis test with only two groups. Mood’s median test compares the medians of two groups. Aligned ranks transformation anova (ART anova) provides nonparametric analysis for a variety of designs. For ordinal data, an alternative is to use cumulative link models, which are described later in this book.
Optional technical note on hypotheses for Mann–Whitney test
See the Kruskal–Wallis Test chapter for more information.
Packages used in this chapter
The packages used in this chapter include:
• psych
• FSA
• lattice
• rcompanion
• coin
• DescTools
• effsize
• exactRankTests
The following commands will install these packages if they are not already installed:
if(!require(psych)){install.packages("psych")}
if(!require(FSA)){install.packages("FSA")}
if(!require(lattice)){install.packages("lattice")}
if(!require(rcompanion)){install.packages("rcompanion")}
if(!require(coin)){install.packages("coin")}
if(!require(DescTools)){install.packages("DescTools")}
if(!require(effsize)){install.packages("effsize")}
if(!require(exactRankTests)){install.packages("exactRankTests")}
Two-sample Mann–Whitney U test example
This example re-visits the Pooh and Piglet data from the Descriptive Statistics with the likert Package chapter.
It answers the question, “Are Pooh's scores significantly different from those of Piglet?”
The Mann–Whitney U test is conducted with the wilcox.test function in the native stats package, which produces a p-value for the hypothesis. First the data are summarized and examined using bar plots for each group.
Data = read.table(header=TRUE, stringsAsFactors=TRUE, text="
Speaker Likert
Pooh 3
Pooh 5
Pooh 4
Pooh 4
Pooh 4
Pooh 4
Pooh 4
Pooh 4
Pooh 5
Pooh 5
Piglet 2
Piglet 4
Piglet 2
Piglet 2
Piglet 1
Piglet 2
Piglet 3
Piglet 2
Piglet 2
Piglet 3
")
### Create a new variable which is the Likert scores as an ordered factor
Data$Likert.f = factor(Data$Likert,
ordered = TRUE)
### Check the data frame
library(psych)
headTail(Data)
str(Data)
summary(Data)
Summarize data treating Likert scores as factors
Note that the variable we want to count is Likert.f, which is a factor variable. Counts for Likert.f are cross tabulated over values of Speaker. The prop.table function translates a table into proportions. The margin=1 option indicates that the proportions are calculated for each row.
xtabs( ~ Speaker + Likert.f,
data = Data)
Likert.f
Speaker 1 2 3 4 5
Piglet 1 6 2 1 0
Pooh 0 0 1 6 3
XT = xtabs( ~ Speaker + Likert.f,
data = Data)
prop.table(XT,
margin = 1)
Likert.f
Speaker 1 2 3 4 5
Piglet 0.1 0.6 0.2 0.1 0.0
Pooh 0.0 0.0 0.1 0.6 0.3
Bar plots of data by group
library(lattice)
histogram(~ Likert.f | Speaker,
data=Data,
layout=c(1,2) # columns and rows of
individual plots
)
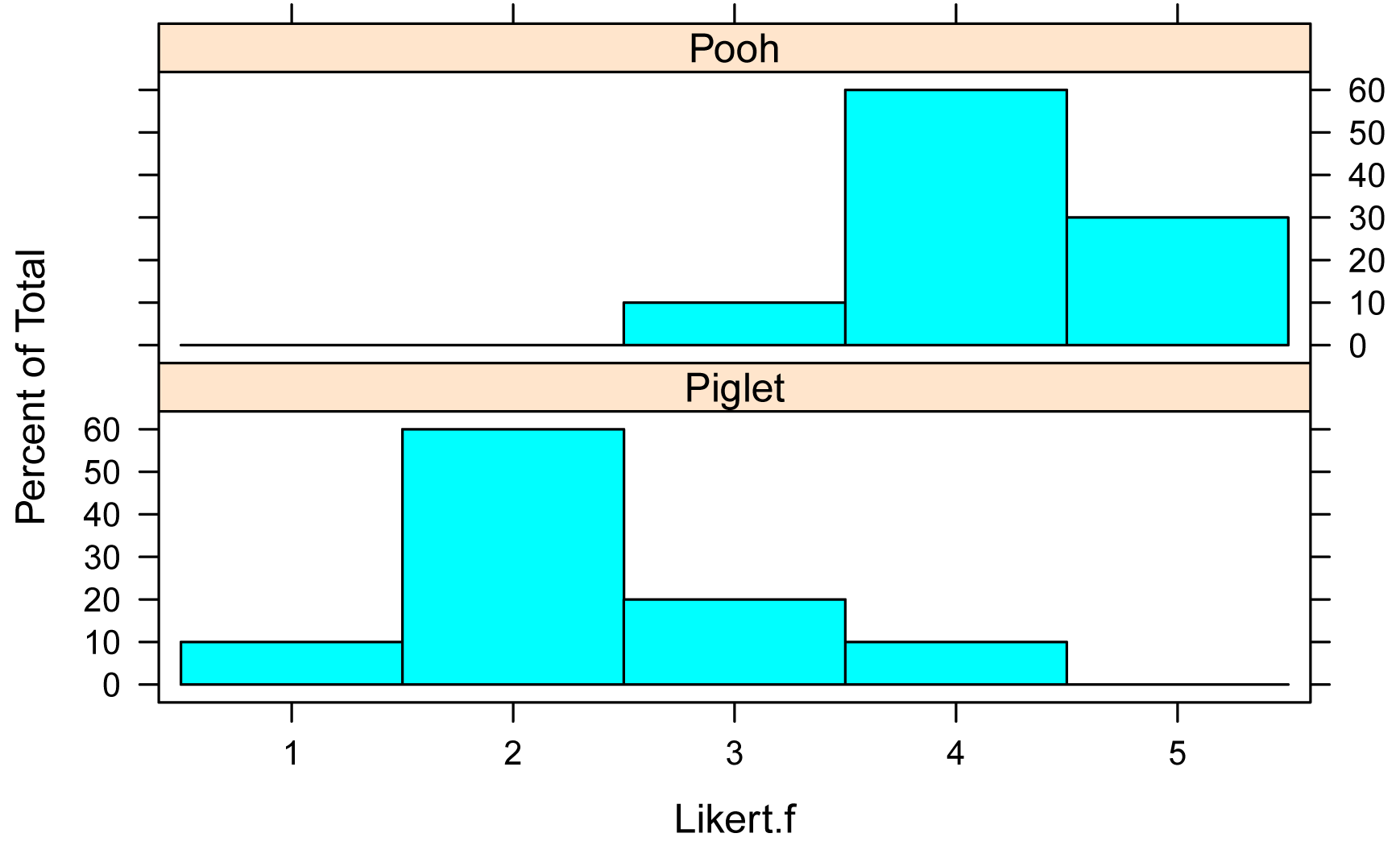
Summarize data treating Likert scores as numeric
library(FSA)
Summarize(Likert ~ Speaker,
data=Data,
digits=3)
Speaker n mean sd min Q1 median Q3 max percZero
1 Piglet 10 2.3 0.823 1 2 2 2.75 4 0
2 Pooh 10 4.2 0.632 3 4 4 4.75 5 0
Two-sample Mann–Whitney U test example
This example uses the formula notation indicating that Likert is the dependent variable and Speaker is the independent variable. The data= option indicates the data frame that contains the variables. For the meaning of other options, see ?wilcox.test.
wilcox.test(Likert ~ Speaker,
data=Data)
Wilcoxon rank sum test with continuity correction
W = 5, p-value = 0.0004713
### You may get a "cannot compute exact p-value
with ties" error.
### You can ignore this or use the exact=FALSE option.
library(coin)
wilcox_test(Likert ~ Speaker, data=Data, distribution = "exact")
Exact Wilcoxon-Mann-Whitney Test
data: Likert by Speaker (Piglet, Pooh)
Z = -3.5358, p-value = 0.0002382
library(coin)
wilcox_test(Likert ~ Speaker, data=Data, distribution =
"approximate")
Approximative Wilcoxon-Mann-Whitney Test
Z = -3.5358, p-value = 2e-04
Another approach is to use the exact test from the exactRankTests package.
library(exactRankTests)
wilcox.exact(Likert ~ Speaker, data=Data, exact=TRUE)
Exact Wilcoxon rank sum test
W = 5, p-value = 0.0002382
Effect size
Statistics of effect size for the Mann–Whitney test report the degree to which one group has data with higher ranks than the other group. They are related to the probability that a value from one group will be greater than a value from the other group. Unlike p-values, they are not affected by sample size.
Vargha and Delaney’s A is relatively easy to understand. It reports the probability that a value from one group will be greater than a value from the other group. A value of 0.50 indicates that the two groups are stochastically equal. A value of 1 indicates that the first group shows complete stochastic domination over the other group, and a value of 0 indicates the complete stochastic domination by the second group.
Cliff’s delta is linearly related to Vargha and Delaney’s A. It ranges from –1 to 1, with 0 indicating stochastic equality of the two groups. 1 indicates that one group shows complete stochastic dominance over the other group, and a value of –1 indicates the complete stochastic domination of the other group. Its absolute value will be numerically equal to Freeman’s theta.
The Glass rank biserial coefficient (rg) is a recommended effect size statistic, and, as far as I can tell, is equivalent to Cliff’s delta. It is included in King, Rosopa, and Minimum (2000).
A common effect size statistic for the Mann–Whitney test is r, which is the z value from the test divided by the total number of observations. This statistic has some drawbacks. Under usual circumstances, it will not range all the way from –1 to 1. It is also affected by sample size. These problems appear to get worse when there are unequal sample sizes between the groups.
Kendall’s tau-b is sometimes used and varies from approximately –1 to 1.
Freeman’s theta and epsilon-squared are usually used when there are more than two groups, with the Kruskal–Wallis test, but can also be employed in the case of two groups.
Interpretation of effect sizes necessarily varies by discipline and the expectations of the experiment, but for behavioral studies, the guidelines proposed by Cohen (1988) are sometimes followed. The following guidelines are based on the literature values and my personal intuition. They should not be considered universal.
Optional technical note: The interpretation values for r below are found commonly in published literature and on the internet. I suspect that this interpretation stems from the adoption of Cohen’s interpretation of values for Pearson’s r. This may not be justified, but it turns out that this interpretation for the r used here is relatively reasonable. The interpretation for tau-b, Freeman’s theta, and epsilon-squared here are based on their values relative to those for r, based on simulated data (5-point Likert items, n per group between 4 and 25). Plots for some of these simulations are shown below.
Interpretations for Vargha and Delaney’s A and Cliff’s delta come from Vargha and Delaney (2000).
|
|
small
|
medium |
large |
|
r |
0.10 – < 0.30 |
0.30 – < 0.50 |
≥ 0.50 |
|
tau-b |
0.10 – < 0.30 |
0.30 – < 0.50 |
≥ 0.50 |
|
Cliff’s delta or rg |
0.11 – < 0.28 |
0.28 – < 0.43 |
≥ 0.43 |
|
Vargha and Delaney’s A |
0.56 – < 0.64 > 0.34 – 0.44 |
0.64 – < 0.71 > 0.29 – 0.34 |
≥ 0.71 ≤ 0.29 |
|
Freeman’s theta |
0.11 – < 0.34 |
0.34 – < 0.58 |
≥ 0.58 |
|
epsilon-squared |
0.01 – < 0.08 |
0.08 – < 0.26 |
≥ 0.26 |
Vargha and Delaney’s A
library(effsize)
VD.A(d = Data$Likert,
f = Data$Speaker)
Vargha and Delaney A
A estimate: 0.05 (large)
library(rcompanion)
vda(Likert ~ Speaker, data=Data)
VDA
0.05
library(rcompanion)
vda(Likert ~ Speaker, data=Data, ci=TRUE)
VDA lower.ci upper.ci
1 0.05 0 0.162
### Note: Bootstrapped confidence interval may
vary.
Glass rank biserial correlation coefficient
library(rcompanion)
wilcoxonRG(x = Data$Likert,
g = Data$Speaker )
rg
-0.9
library(rcompanion)
wilcoxonRG(x = Data$Likert,
g = Data$Speaker,
ci = TRUE)
rg lower.ci upper.ci
1 -0.9 -1 -0.697
### Note: Bootstrapped confidence interval may vary.
Cliff’s delta
library(effsize)
cliff.delta(d = Data$Likert,
f = Data$Speaker)
Cliff's Delta
delta estimate: -0.9 (large)
95 percent confidence interval:
lower upper
-0.9801533 -0.5669338
library(rcompanion)
cliffDelta(Likert ~ Speaker, data=Data)
Cliff.delta
-0.9
library(rcompanion)
cliffDelta(Likert ~ Speaker, data=Data, ci=TRUE)
Cliff.delta lower.ci upper.ci
1 -0.9 -1 -0.67
### Note: Bootstrapped confidence interval may
vary.
r
library(rcompanion)
wilcoxonR(x = Data$Likert,
g = Data$Speaker)
r
0.791
library(rcompanion)
wilcoxonR(x = Data$Likert,
g = Data$Speaker,
ci = TRUE)
r lower.ci upper.ci
1 0.791 0.602 0.897
### Note: Bootstrapped confidence interval may
vary.
Agresti's Generalized Odds Ratio for Stochastic Dominance
library(rcompanion)
wilcoxonOR(Likert ~ Speaker, data=Data)
OR
1 0.011
wilcoxonOR(Likert ~ Speaker, data=Data, ci=TRUE)
OR lower.ci upper.ci
1 0.011 0 0.073
### Note: Bootstrapped confidence interval may
vary.
Grissom and Kim's Probability of Superiority
library(rcompanion)
wilcoxonPS(Likert ~ Speaker, data=Data)
PS
1 0.01
wilcoxonPS(Likert ~ Speaker, data=Data, ci=TRUE)
1 0.01 0 0.06
### Note: Bootstrapped confidence interval may
vary.
tau-b
library(DescTools)
KendallTauB(x = Data$Likert,
y = as.numeric(Data$Speaker))
[1] 0.7397954
library(DescTools)
KendallTauB(x = Data$Likert,
y = as.numeric(Data$Speaker),
conf.level = 0.95)
tau_b lwr.ci upr.ci
0.7397954 0.6074611 0.8721298
Freeman’s theta
library(rcompanion)
freemanTheta(x = Data$Likert,
g = Data$Speaker)
Freeman.theta
0.9
library(rcompanion)
freemanTheta(x = Data$Likert,
g = Data$Speaker,
ci = TRUE)
Freeman.theta lower.ci upper.ci
1 0.9 0.688 1
### Note: Bootstrapped confidence interval may
vary.
epsilon-squared
library(rcompanion)
epsilonSquared(x = Data$Likert,
g = Data$Speaker)
epsilon.squared
0.658
library(rcompanion)
epsilonSquared(x = Data$Likert,
g = Data$Speaker,
ci = TRUE)
epsilon.squared lower.ci upper.ci
1 0.658 0.383 0.842
### Note: Bootstrapped confidence interval may
vary.
Optional: extracting the z value
The wilcox.test function calculates the z value but doesn’t report it in the output. It is sometimes more useful to report a z value than the U statistic or the W statistic that R reports. There are a couple of different ways to extract the z value.
A = c(2, 4, 6, 8, 10, 12)
B = c(7, 9, 11, 13, 15, 17)
library(rcompanion)
wilcoxonZ(A, B)
z
-1.92
Y = c(A, B)
Group = factor(c(rep("A", length(A)), rep("B", length(B))))
library(coin)
wilcox_test(Y ~ Group)
Asymptotic Wilcoxon-Mann-Whitney Test
Z = -1.9215, p-value = 0.05466
Optional: Comparison among effect size statistics
The follow plots show the relationship among some effect size statistics discussed in this chapter. Data were 5-point Likert item responses, with n per group between 4 and 25.
Freeman’s theta was mostly linearly related to r, with variation depending on sample size and data values. In the second figure below, the colors indicate interpretation of less-than-small, small, medium, and large as the blue becomes darker.


The relationship of epsilon-squared and Freeman’s theta was curvilineal, with variation depending on sample size and data values. In the second figure below, the colors indicate interpretation of less-than-small, small, medium, and large as the blue becomes darker

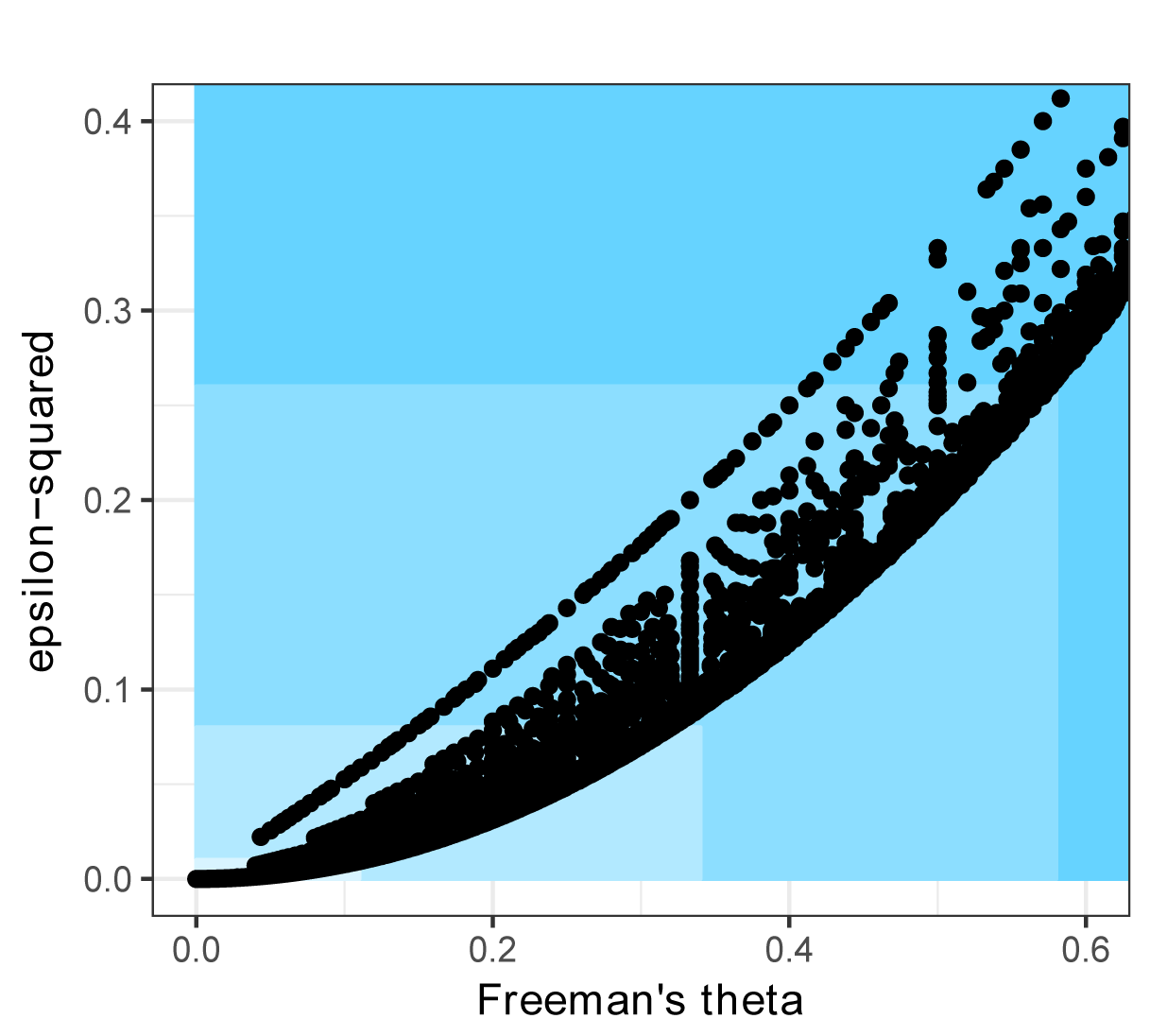
Kendall’s tau-b was relatively closely linearly related to r, up to a value of about 0.88. In second figure below, the colors indicate interpretation of less-than-small, small, medium, and large as the blue becomes darker.


References
Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, 2nd Edition. Routledge.
King, B.M., P.J. Rosopa, and E.W. Minium. 2000. Statistical Reasoning in the Behavioral Sciences, 6th. Wiley.
Vargha, A. and H.D. Delaney. A Critique and Improvement of the CL Common Language Effect Size Statistics of McGraw and Wong. 2000. Journal of Educational and Behavioral Statistics 25(2):101–132.
Exercises J
1. Considering Pooh and Piglet’s data,
a. What was the median score for each instructor?
b. What were the first and third quartiles for each
instructor’s scores?
c. According to the Mann–Whitney test, is there a difference
in scores between the instructors?
d. What was the value of Vargha and Delaney’s A for the
effect size for these data?
e. How do you interpret this value? (What does it mean? And is
the standard interpretation in terms of “small”, “medium”, or “large”?)
f. How would you summarize the results of the descriptive statistics and tests? Include practical considerations of any differences.
2. Brian and Stewie Griffin want to assess the education level of students in
their courses on creative writing for adults. They want to know the median
education level for each class, and if the education level of the classes were
different between instructors.
They used the following table to code his data.
Code Abbreviation Level
1 < HS Less than high school
2 HS High school
3 BA Bachelor’s
4 MA Master’s
5 PhD Doctorate
The following are the course data.
Instructor Student Education
'Brian Griffin' a 3
'Brian Griffin' b 2
'Brian Griffin' c 3
'Brian Griffin' d 3
'Brian Griffin' e 3
'Brian Griffin' f 3
'Brian Griffin' g 4
'Brian Griffin' h 5
'Brian Griffin' i 3
'Brian Griffin' j 4
'Brian Griffin' k 3
'Brian Griffin' l 2
'Stewie Griffin' m 4
'Stewie Griffin' n 5
'Stewie Griffin' o 4
'Stewie Griffin' p 4
'Stewie Griffin' q 4
'Stewie Griffin' r 4
'Stewie Griffin' s 3
'Stewie Griffin' t 5
'Stewie Griffin' u 4
'Stewie Griffin' v 4
'Stewie Griffin' w 3
'Stewie Griffin' x 2
For each of the following, answer the question, and show the output from the analyses you used to answer the question.
a. What was the median education level for each instructor? (Be sure to report the education level, not just the numeric code!)
b. What were the first and third quartiles for education level for each instructor?
c. According to the Mann–Whitney test, is there a difference in scores between the instructors?
d. What was the value of Vargha and Delaney’s A for the
effect size for these data?
e. How do you interpret this value? (What does it mean? And is
the standard interpretation in terms of “small”, “medium”, or “large”?)
f. Plot Brian and Stewie’s data in a way that helps you visualize the data. Do the results reflect what you would expect from looking at the plot?
g. How would you summarize the results of the descriptive statistics and tests? Include your practical interpretation.
![Cohansey River, Fairfield, New Jersey [banner]](images/banner.jpg)